How to brute force a tower with blocks.

Today we have a simple volume problem. Imagine you are stacking cube blocks to make a tower. on the bottom you have n blocks with a total volume of n^3, the next level has n-1 blocks and volume (n-1)^3… until the top with 1 block and a volume of 1^3.
Given a total volume, m, the task is to calculate the value of n if it exists or return -1 if there is no value of n that works.
Thoughts
m is the total volume, i.e. the sum of every layer, and each successive layer is less than the preceding by 1.
So we can think of it as;
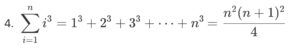
Let’s brute force a tower
We can brute force this pretty easily by just iterating and checking. i.e.
pub fn find_nb(m: u64) -> i32 {
let mut i:u64 = 1;
let mut sum: u64 = 0;
loop {
sum = sum + i.pow(3);
match sum.cmp(&m) {
Ordering::Less => {
i = i + 1;
},
Ordering::Equal => return i as i32,
Ordering::Greater => return -1
}
}
}
Code language: Rust (rust)Looking at the equation image above, you will notice that we have a handy formula. So in theory we can potentially reduce processing time to constant time if we can calculate n based on m.
But I’m not going to do that today, mainly because reasons. Anyway, that’s it for today. Let me know on Twitter how y’all solved this, @phoexer. Happy coding.
Recommended Posts

How to brute force a tower with blocks.
Today I am working on a summation problem made to look like building a tower out of cubic bricks. It’s fun to brute force sometimes.

Two-Sum Problem
Coming back to Rust code after a bit of a hiatus with a simple problem… The Two-sum problem. Finding numbers in an array. Yay, fun.

Lyrics out of context: I Salute You
King Pinn: I Salute You. I’m driving halfway across the country and this song is on repeat. Rest in Peace Tonderai Makoni. You were awesome.

I’m back
After a few weeks off I’m back to business. This is just an update post detailing plans for the rest of the year.

Day 13: RSA Encryption
At last we finally have the great reveal, our mystery project was implementing RSA encryption in rust.
